Spider: Euler angle conventions
Euler angles in SPIDER & Web
The Euler angles in SPIDER & Web are defined as three successive rotations in a right hand coordinate system. First, the object is rotated CLOCKWISE round the Z-axis (angle 'phi') and then it is rotated CLOCKWISE around the Y-axis (angle 'theta') and finally, it is rotated CLOCKWISE around the Z-axis (angle 'psi'). All rotations are done around axes of the SPACE coordinate system and direction of rotation is determined by looking to the origin.
Note: If a volume is displayed in Web as slices, the observed rotations will be, COUNTERCLOCKWISE for 'phi' and 'psi' rotations around Z-axis and CLOCKWISE for 'theta' rotation around Y-axis. This is due to the way a SPIDER volume is displayed in Web.
The rotation matrices used are defined as:
v = Rv', where R is the matrix for transforming vector v' to vector v.
R = R(psi) * R(theta) * R(phi)
R(psi) = cos(psi) sin(psi) 0
-sin(psi) cos(psi) 0
0 0 1
R(theta) = cos(theta) 0 -sin(theta)
0 1 0
sin(theta) 0 cos(theta)
R(phi) = cos(phi) sin(phi) 0
-sin(phi) cos(phi) 0
0 0 1
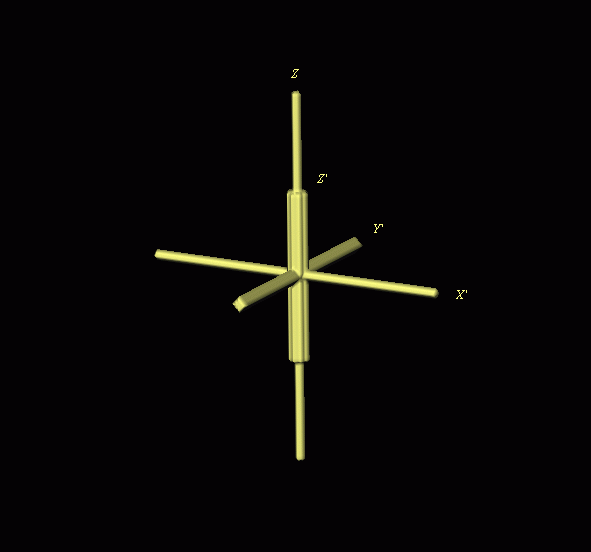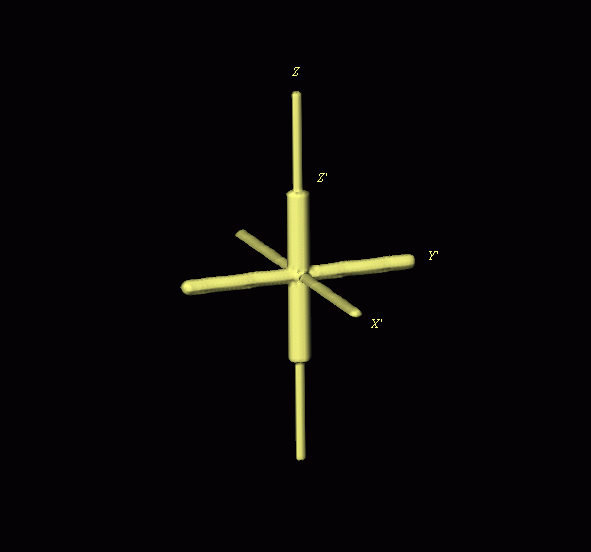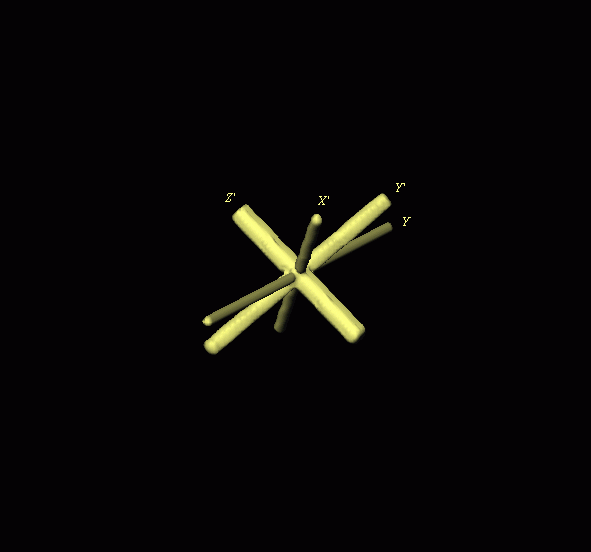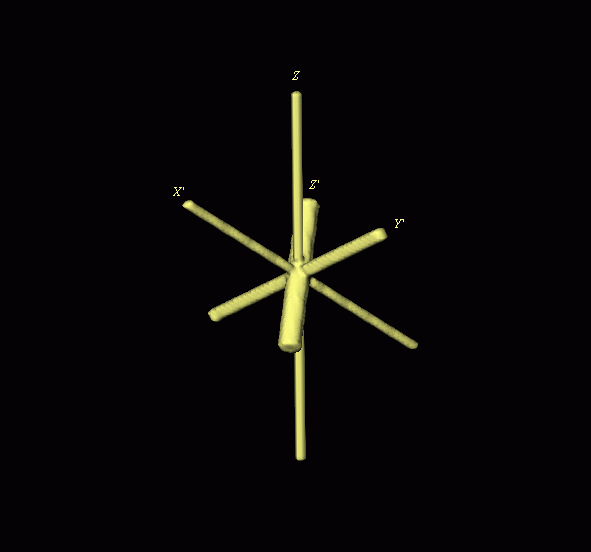
Rotation by: Phi: 40 Theta: 50 & Psi: 70
Animation Notes:
An object consisting of 3 cylinders of different lengths and diameters that coincide with the three orthogonal axes was created using SPIDER.
The RT 3D SPIDER operation was used to rotate this object by Phi: 40 Theta: 50 & Psi: 70. A cylinder parallel to the rotation axis is embedded to the object before each rotation. Each rotation is done in 10 incremental steps to capture the position of the object for making the illustration. X', Y' and Z' are in the body coordinate system whereas Y and Z are in the space coordinate system.
Note: This is a mirror of the Spider documentation page regarding Euler angles in Spider & Web, as downloaded Oct 19th, 2010. Note that this documentation is licensed under a Creative Commons Attribution License 2.5. See this page for the original licensing terms.